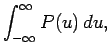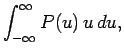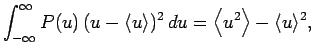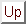

Next: Exercises
Up: Probability Theory
Previous: Mean, Variance, and Standard
Suppose, now, that the variable 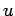 can take on a continuous range of possible
values. In general, we expect the probability that
can take on a continuous range of possible
values. In general, we expect the probability that 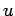 takes on a value
in the range
takes on a value
in the range 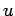 to
to 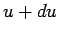 to be directly proportional to
to be directly proportional to 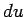 ,
in the limit that
,
in the limit that
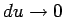 . In other words,
. In other words,
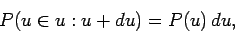 |
(23) |
where 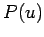 is known as the probability density.
The earlier results (5), (12), and (19) generalize in a
straightforward manner to give
is known as the probability density.
The earlier results (5), (12), and (19) generalize in a
straightforward manner to give
respectively.
Subsections
Richard Fitzpatrick
2010-07-20