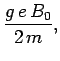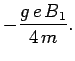Next: Perturbation Expansion
Up: Time-Dependent Perturbation Theory
Previous: Two-State System
Consider a system consisting of a spin one-half particle with no orbital
angular momentum (e.g., a bound electron)
placed in a uniform 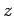 -directed magnetic field, and then subject
to a small time-dependent magnetic field rotating in the
-directed magnetic field, and then subject
to a small time-dependent magnetic field rotating in the 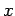 -
-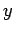 plane at the
angular frequency
plane at the
angular frequency 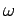 .
Thus,
.
Thus,
![\begin{displaymath}
{\bf B} = B_0 {\bf e}_z + B_1 \left[\cos(\omega t) {\bf e}_x + \sin(\omega t) {\bf e}_y\right],
\end{displaymath}](img2443.png) |
(1045) |
where 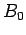 and
and 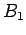 are constants, with
are constants, with 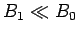 . The rotating
magnetic field usually represents the magnetic component of an electromagnetic wave propagating along the
. The rotating
magnetic field usually represents the magnetic component of an electromagnetic wave propagating along the 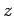 -axis. In this system,
the electric component of the wave has no effect. The Hamiltonian
is written
-axis. In this system,
the electric component of the wave has no effect. The Hamiltonian
is written
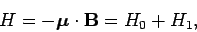 |
(1046) |
where
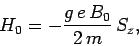 |
(1047) |
and
![\begin{displaymath}
H_1 = -\frac{g e B_1}{2 m} \left[\cos(\omega t) S_x+ \sin(\omega t) S_y\right].
\end{displaymath}](img2448.png) |
(1048) |
Here, 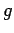 and
and 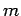 are the gyromagnetic ratio [see Eq. (1004)] and mass of the particle in question, respectively.
are the gyromagnetic ratio [see Eq. (1004)] and mass of the particle in question, respectively.
The eigenstates of the unperturbed Hamiltonian are the ``spin up'' and ``spin
down'' states, denoted 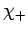 and
and 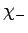 , respectively. Of course,
these states are the eigenstates of
, respectively. Of course,
these states are the eigenstates of  corresponding to the
eigenvalues
corresponding to the
eigenvalues 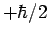 and
and 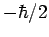 respectively (see Sect. 10).
Thus, we have
respectively (see Sect. 10).
Thus, we have
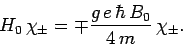 |
(1049) |
The time-dependent Hamiltonian can be written
![\begin{displaymath}
H_1 = - \frac{g e B_1}{4 m}\left[\exp( {\rm i} \omega t) S_- +
\exp(-{\rm i} \omega t) S_+\right],
\end{displaymath}](img2450.png) |
(1050) |
where 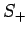 and
and 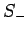 are the conventional raising and lowering
operators for spin angular momentum (see Sect. 10). It follows
that
are the conventional raising and lowering
operators for spin angular momentum (see Sect. 10). It follows
that
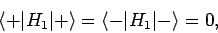 |
(1051) |
and
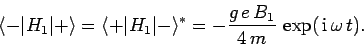 |
(1052) |
It can be seen that this system is exactly the same as the two-state
system discussed in the previous subsection, provided that the
make the following indentifications:
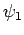 |
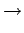 |
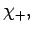 |
(1053) |
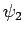 |
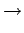 |
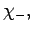 |
(1054) |
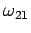 |
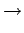 |
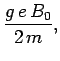 |
(1055) |
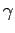 |
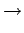 |
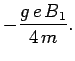 |
(1056) |
The resonant frequency, 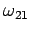 , is simply the spin precession
frequency in a uniform magnetic field of strength
, is simply the spin precession
frequency in a uniform magnetic field of strength 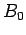 (see Sect. 10.6). In the absence of the perturbation, the
expectation values of
(see Sect. 10.6). In the absence of the perturbation, the
expectation values of 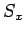 and
and 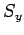 oscillate because of the spin
precession, but the expectation value of
oscillate because of the spin
precession, but the expectation value of  remains invariant. If we
now apply a magnetic perturbation rotating at the resonant frequency then,
according to the analysis of the previous subsection, the system undergoes
a succession of spin flips,
remains invariant. If we
now apply a magnetic perturbation rotating at the resonant frequency then,
according to the analysis of the previous subsection, the system undergoes
a succession of spin flips,
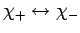 , in addition
to the spin precession. We also know that if the oscillation frequency
of the applied field is very different from the resonant frequency
then there is virtually zero probability of the field triggering a
spin flip. The width of the resonance (in frequency) is determined by
the strength of the oscillating magnetic perturbation. Experimentalists
are able to measure the gyromagnetic ratios of spin one-half
particles to a high degree of accuracy by placing the particles
in a uniform magnetic field of known strength, and then subjecting them to an oscillating
magnetic field whose frequency is gradually scanned. By determining the
resonant frequency (i.e., the frequency at which the particles
absorb energy from the oscillating field), it is possible
to determine the gyromagnetic ratio (assuming that the mass is known).
, in addition
to the spin precession. We also know that if the oscillation frequency
of the applied field is very different from the resonant frequency
then there is virtually zero probability of the field triggering a
spin flip. The width of the resonance (in frequency) is determined by
the strength of the oscillating magnetic perturbation. Experimentalists
are able to measure the gyromagnetic ratios of spin one-half
particles to a high degree of accuracy by placing the particles
in a uniform magnetic field of known strength, and then subjecting them to an oscillating
magnetic field whose frequency is gradually scanned. By determining the
resonant frequency (i.e., the frequency at which the particles
absorb energy from the oscillating field), it is possible
to determine the gyromagnetic ratio (assuming that the mass is known).



Next: Perturbation Expansion
Up: Time-Dependent Perturbation Theory
Previous: Two-State System
Richard Fitzpatrick
2010-07-20
![]() and
and ![]() , respectively. Of course,
these states are the eigenstates of
, respectively. Of course,
these states are the eigenstates of ![]() corresponding to the
eigenvalues
corresponding to the
eigenvalues ![]() and
and ![]() respectively (see Sect. 10).
Thus, we have
respectively (see Sect. 10).
Thus, we have