


Next: Spontaneous Emission
Up: Time-Dependent Perturbation Theory
Previous: Electromagnetic Radiation
Electric Dipole Approximation
In general, the wavelength of the type of electromagnetic
radiation which induces, or is emitted during, transitions between different
atomic energy levels is much larger than the typical size of an atom.
Thus,
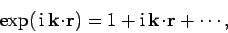 |
(1109) |
can be approximated by its first term, unity. This approach is
known as the electric dipole approximation.
It follows that
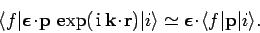 |
(1110) |
Now, it is readily demonstrated that
![\begin{displaymath}[{\bf r}, H_0]= \frac{{\rm i} \hbar {\bf p}}{m_e},
\end{displaymath}](img2578.png) |
(1111) |
so
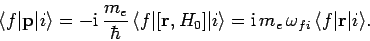 |
(1112) |
Thus, our previous expressions for the transition rates for radiation induced absorption and
stimulated emission reduce to
respectively. Here,
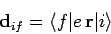 |
(1115) |
is the effective electric dipole moment of the atom when making a
transition from state 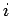 to state
to state 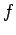 .
.
Equations (1113) and (1114) give the transition rates
for absorption and stimulated emission, respectively, induced by
a linearly polarized plane-wave. Actually, we are more interested in the
transition rates induced by unpolarized isotropic radiation. To obtain
these we must average Eqs. (1113) and (1114)
over all possible polarizations and propagation directions of the wave.
To facilitate this process, we can define a set of Cartesian coordinates
such that the wavevector 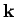 , which specifies the direction
of wave propagation, points along the
, which specifies the direction
of wave propagation, points along the 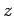 -axis, and the vector
-axis, and the vector 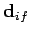 ,
which specifies the direction of the atomic dipole moment, lies
in the
,
which specifies the direction of the atomic dipole moment, lies
in the 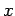 -
-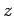 plane. It follows that the vector
plane. It follows that the vector
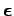 , which
specifies the direction of wave polarization, must lie
in the
, which
specifies the direction of wave polarization, must lie
in the 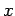 -
-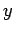 plane, since it has to be orthogonal to
plane, since it has to be orthogonal to 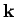 .
Thus, we can write
.
Thus, we can write
which implies that
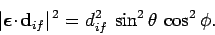 |
(1119) |
We must now average the above quantity over all possible values of
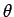 and
and 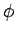 . Thus,
. Thus,
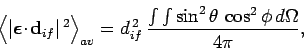 |
(1120) |
where
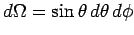 , and the integral is taken over all
solid angle. It is easily demonstrated that
, and the integral is taken over all
solid angle. It is easily demonstrated that
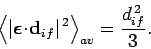 |
(1121) |
Here, 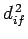 stands for
stands for
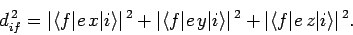 |
(1122) |
Hence, the transition rates
for absorption and stimulated emission induced by
unpolarized isotropic radiation are
respectively.



Next: Spontaneous Emission
Up: Time-Dependent Perturbation Theory
Previous: Electromagnetic Radiation
Richard Fitzpatrick
2010-07-20
![]() , which specifies the direction
of wave propagation, points along the
, which specifies the direction
of wave propagation, points along the ![]() -axis, and the vector
-axis, and the vector ![]() ,
which specifies the direction of the atomic dipole moment, lies
in the
,
which specifies the direction of the atomic dipole moment, lies
in the ![]() -
-![]() plane. It follows that the vector
plane. It follows that the vector
![]() , which
specifies the direction of wave polarization, must lie
in the
, which
specifies the direction of wave polarization, must lie
in the ![]() -
-![]() plane, since it has to be orthogonal to
plane, since it has to be orthogonal to ![]() .
Thus, we can write
.
Thus, we can write