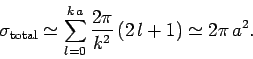Next: Low Energy Scattering
Up: Scattering Theory
Previous: Determination of Phase-Shifts
Let us test out this scheme using a particularly simple example. Consider
scattering by a hard sphere, for which the potential is infinite
for 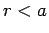 , and zero for
, and zero for 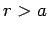 . It follows that
. It follows that 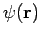 is
zero in the region
is
zero in the region 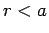 , which implies that
, which implies that 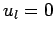 for all
for all 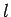 .
Thus,
.
Thus,
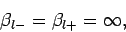 |
(1319) |
for all 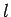 . Equation (1312) thus gives
. Equation (1312) thus gives
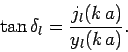 |
(1320) |
Consider the 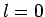 partial wave, which is usually referred to as the
partial wave, which is usually referred to as the 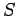 -wave.
Equation (1320) yields
-wave.
Equation (1320) yields
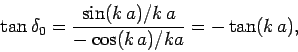 |
(1321) |
where use has been made of Eqs. (1289) and (1290). It follows that
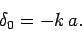 |
(1322) |
The 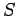 -wave radial wave function
is [see Eq. (1310)]
-wave radial wave function
is [see Eq. (1310)]
The corresponding radial wavefunction for the incident wave
takes the form [see Eq. (1298)]
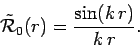 |
(1324) |
Thus, the actual 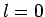 radial wavefunction is similar to the
incident
radial wavefunction is similar to the
incident 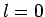 wavefunction, except that it is phase-shifted by
wavefunction, except that it is phase-shifted by 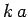 .
.
Let us examine the low and high energy asymptotic limits of 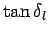 .
Low energy implies that
.
Low energy implies that 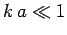 . In this regime, the spherical Bessel functions
reduce to:
. In this regime, the spherical Bessel functions
reduce to:
where
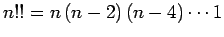 . It follows that
. It follows that
![\begin{displaymath}
\tan\delta_l = \frac{-(k a)^{2 l+1}}{(2 l+1) [(2 l-1)!!]^{ 2}}.
\end{displaymath}](img2977.png) |
(1327) |
It is clear that we can neglect 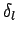 , with
, with 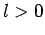 , with respect to
, with respect to
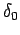 . In other words, at low energy only
. In other words, at low energy only 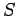 -wave scattering
(i.e., spherically symmetric scattering) is important. It follows
from Eqs. (1266), (1306), and (1322) that
-wave scattering
(i.e., spherically symmetric scattering) is important. It follows
from Eqs. (1266), (1306), and (1322) that
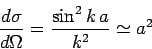 |
(1328) |
for 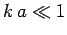 . Note that the total cross-section
. Note that the total cross-section
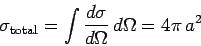 |
(1329) |
is four times the geometric cross-section 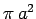 (i.e., the cross-section for classical particles bouncing off a
hard sphere of radius
(i.e., the cross-section for classical particles bouncing off a
hard sphere of radius 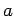 ).
However,
low energy scattering implies relatively long wavelengths, so we would not
expect to obtain the classical result in this limit.
).
However,
low energy scattering implies relatively long wavelengths, so we would not
expect to obtain the classical result in this limit.
Consider the high energy limit 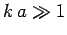 . At high energies, all partial
waves up to
. At high energies, all partial
waves up to
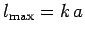 contribute significantly to
the scattering cross-section. It follows from Eq. (1308) that
contribute significantly to
the scattering cross-section. It follows from Eq. (1308) that
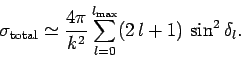 |
(1330) |
With so many 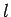 values contributing, it is legitimate to replace
values contributing, it is legitimate to replace
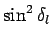 by its average value
by its average value 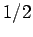 . Thus,
. Thus,
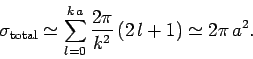 |
(1331) |
This is twice the classical result, which is somewhat surprizing,
since we might expect to obtain the classical result in the short
wavelength limit. For hard sphere scattering, incident waves with
impact parameters less than 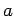 must be deflected. However, in order to
produce a ``shadow'' behind the sphere, there must also be some scattering
in the forward direction in order to produce
destructive interference with the incident plane-wave. In fact, the
interference is not completely destructive, and the shadow has a bright
spot (the so-called ``Poisson spot'') in the forward direction. The effective cross-section associated with
this bright spot is
must be deflected. However, in order to
produce a ``shadow'' behind the sphere, there must also be some scattering
in the forward direction in order to produce
destructive interference with the incident plane-wave. In fact, the
interference is not completely destructive, and the shadow has a bright
spot (the so-called ``Poisson spot'') in the forward direction. The effective cross-section associated with
this bright spot is 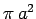 which, when combined with the
cross-section for classical reflection,
which, when combined with the
cross-section for classical reflection, 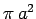 , gives the actual
cross-section of
, gives the actual
cross-section of 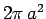 .
.



Next: Low Energy Scattering
Up: Scattering Theory
Previous: Determination of Phase-Shifts
Richard Fitzpatrick
2010-07-20
![]() partial wave, which is usually referred to as the
partial wave, which is usually referred to as the ![]() -wave.
Equation (1320) yields
-wave.
Equation (1320) yields
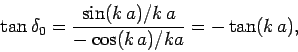
![$\displaystyle \exp(-{\rm i} k a) \frac{[\cos (k a) \sin (k r)
-\sin (k a) \cos (k r)]}{k r}$](img2965.png)
![$\displaystyle \exp(-{\rm i} k a) \frac{ \sin[k (r-a)]}{k r}.$](img2966.png)
![]() .
Low energy implies that
.
Low energy implies that ![]() . In this regime, the spherical Bessel functions
reduce to:
. In this regime, the spherical Bessel functions
reduce to:
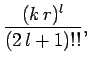
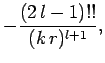
![\begin{displaymath}
\tan\delta_l = \frac{-(k a)^{2 l+1}}{(2 l+1) [(2 l-1)!!]^{ 2}}.
\end{displaymath}](img2977.png)
![]() . At high energies, all partial
waves up to
. At high energies, all partial
waves up to
![]() contribute significantly to
the scattering cross-section. It follows from Eq. (1308) that
contribute significantly to
the scattering cross-section. It follows from Eq. (1308) that