


Next: Classical Interference of Light
Up: Wave-Particle Duality
Previous: Photoelectric Effect
According to Einstein's quantum theory of light, a monochromatic light wave of angular
frequency 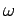 , propagating through a vacuum, can be thought of
as a stream of particles, called photons, of energy
, propagating through a vacuum, can be thought of
as a stream of particles, called photons, of energy
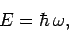 |
(60) |
where
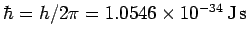 . Since
classical light waves propagate at the fixed velocity
. Since
classical light waves propagate at the fixed velocity 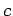 , it stands to reason that photons
must also move at this velocity. Now, according to Einstein's special theory
of relativity, only massless particles can move at the speed of light in vacuum. Hence,
photons must be massless. Special relativity also gives the following
relationship between the energy
, it stands to reason that photons
must also move at this velocity. Now, according to Einstein's special theory
of relativity, only massless particles can move at the speed of light in vacuum. Hence,
photons must be massless. Special relativity also gives the following
relationship between the energy 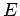 and the momentum
and the momentum 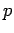 of a massless
particle,
of a massless
particle,
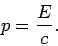 |
(61) |
Note that the above relation is consistent with Eq. (57), since
if light is made up of a stream of photons, for which 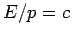 , then the momentum density of light must be the energy density divided by
, then the momentum density of light must be the energy density divided by 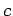 .
It follows from the previous two equations that photons carry momentum
.
It follows from the previous two equations that photons carry momentum
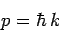 |
(62) |
along their direction of motion,
since 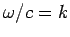 for a light wave [see Eq. (50)].
for a light wave [see Eq. (50)].



Next: Classical Interference of Light
Up: Wave-Particle Duality
Previous: Photoelectric Effect
Richard Fitzpatrick
2010-07-20