


Next: Expectation Values and Variances
Up: Fundamentals of Quantum Mechanics
Previous: Schrödinger's Equation
Now, a probability is a real number between 0 and 1. An outcome
of a measurement which has a probability 0 is an impossible outcome, whereas an
outcome which has a probability 1 is a certain outcome. According to
Eq. (138), the probability of a measurement of 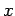 yielding
a result between
yielding
a result between 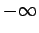 and
and 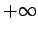 is
is
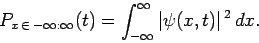 |
(139) |
However, a measurement of 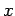 must yield a value between
must yield a value between 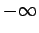 and
and
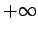 , since the particle has to be located somewhere. It follows that
, since the particle has to be located somewhere. It follows that
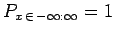 , or
, or
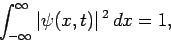 |
(140) |
which is generally known as the normalization condition for the
wavefunction.
For example, suppose that we wish to normalize the wavefunction of
a Gaussian wave packet, centered on 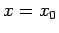 , and of characteristic
width
, and of characteristic
width 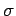 (see Sect. 3.12): i.e.,
(see Sect. 3.12): i.e.,
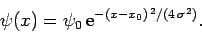 |
(141) |
In order to determine the normalization constant 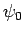 , we simply substitute
Eq. (141) into Eq. (140), to obtain
, we simply substitute
Eq. (141) into Eq. (140), to obtain
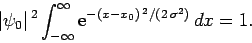 |
(142) |
Changing the variable of integration to
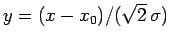 , we get
, we get
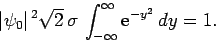 |
(143) |
However,
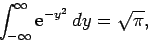 |
(144) |
which implies that
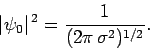 |
(145) |
Hence, a general normalized Gaussian wavefunction takes the form
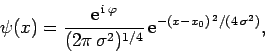 |
(146) |
where 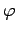 is an arbitrary real phase-angle.
is an arbitrary real phase-angle.
Now, it is important to demonstrate that if a wavefunction is initially
normalized then it stays normalized as it evolves in time according
to Schrödinger's equation. If this is not the case then
the probability interpretation of the wavefunction is untenable, since it
does not make sense for the probability that a measurement of 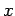 yields any possible outcome (which is, manifestly, unity) to change in time.
Hence, we require that
yields any possible outcome (which is, manifestly, unity) to change in time.
Hence, we require that
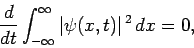 |
(147) |
for wavefunctions satisfying Schrödinger's equation.
The above equation gives
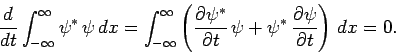 |
(148) |
Now, multiplying Schrödinger's equation by
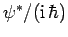 ,
we obtain
,
we obtain
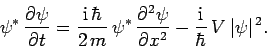 |
(149) |
The complex conjugate of this expression yields
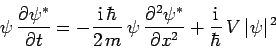 |
(150) |
[since
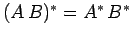 ,
,
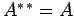 , and
, and 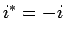 ].
Summing the previous two equations, we get
].
Summing the previous two equations, we get
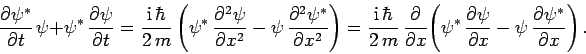 |
(151) |
Equations (148) and (151) can be combined to
produce
![\begin{displaymath}
\frac{d}{dt}\int_{-\infty}^{\infty}\vert\psi\vert^{ 2} dx=...
...{\partial\psi^\ast}{\partial x}\right]_{-\infty}^{\infty} = 0.
\end{displaymath}](img478.png) |
(152) |
The above equation is satisfied provided
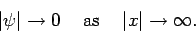 |
(153) |
However, this is a necessary condition for the integral on the left-hand
side of Eq. (140) to converge. Hence, we conclude that
all wavefunctions which are square-integrable [i.e., are such that the integral in Eq. (140) converges] have the property
that if the normalization condition (140) is satisfied at one instant
in time then it is satisfied at all subsequent times.
It is also possible to demonstrate, via very similar analysis to the above, that
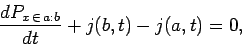 |
(154) |
where
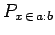 is defined in Eq. (138), and
is defined in Eq. (138), and
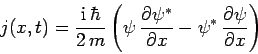 |
(155) |
is known as the probability current. Note that 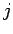 is real.
Equation (154) is a probability conservation equation.
According to this equation, the probability of a measurement
of
is real.
Equation (154) is a probability conservation equation.
According to this equation, the probability of a measurement
of 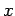 lying in the interval
lying in the interval 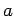 to
to 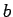 evolves in time due to the
difference between the flux of probability into the interval [i.e.,
evolves in time due to the
difference between the flux of probability into the interval [i.e., 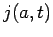 ],
and that out of the interval [i.e.,
],
and that out of the interval [i.e., 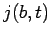 ].
Here, we are interpreting
].
Here, we are interpreting 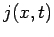 as the flux of probability in the
as the flux of probability in the 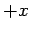 -direction at position
-direction at position 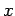 and time
and time 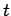 .
.
Note, finally, that not all wavefunctions can be normalized according to the scheme set out in Eq. (140). For instance, a plane wave wavefunction
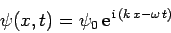 |
(156) |
is not square-integrable, and, thus, cannot be normalized.
For such wavefunctions, the best we can say is that
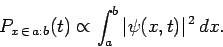 |
(157) |
In the following, all wavefunctions are assumed to be square-integrable and
normalized, unless otherwise stated.



Next: Expectation Values and Variances
Up: Fundamentals of Quantum Mechanics
Previous: Schrödinger's Equation
Richard Fitzpatrick
2010-07-20
![]() , and of characteristic
width
, and of characteristic
width ![]() (see Sect. 3.12): i.e.,
(see Sect. 3.12): i.e.,
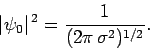
![]() yields any possible outcome (which is, manifestly, unity) to change in time.
Hence, we require that
yields any possible outcome (which is, manifestly, unity) to change in time.
Hence, we require that
![\begin{displaymath}
\frac{d}{dt}\int_{-\infty}^{\infty}\vert\psi\vert^{ 2} dx=...
...{\partial\psi^\ast}{\partial x}\right]_{-\infty}^{\infty} = 0.
\end{displaymath}](img478.png)