


Next: Exercises
Up: Fundamentals of Quantum Mechanics
Previous: Continuous Eigenvalues
Stationary States
An eigenstate of the energy operator
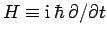 corresponding to the eigenvalue
corresponding to the eigenvalue 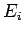 satisfies
satisfies
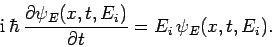 |
(293) |
It is evident that this equation can be solved by writing
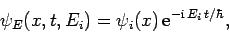 |
(294) |
where 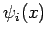 is a properly normalized stationary (i.e., non-time-varying) wavefunction. The wavefunction
is a properly normalized stationary (i.e., non-time-varying) wavefunction. The wavefunction
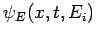 corresponds to a so-called stationary state, since
the probability density
corresponds to a so-called stationary state, since
the probability density
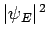 is non-time-varying. Note that
a stationary state is associated with a unique value for the energy.
Substitution of the above expression into Schrödinger's equation (137) yields the equation satisfied by the
stationary wavefunction:
is non-time-varying. Note that
a stationary state is associated with a unique value for the energy.
Substitution of the above expression into Schrödinger's equation (137) yields the equation satisfied by the
stationary wavefunction:
![\begin{displaymath}
\frac{\hbar^2}{2 m} \frac{d^2 \psi_i}{d x^2} =
\left[V(x)-E_i\right]\psi_i.
\end{displaymath}](img740.png) |
(295) |
This is known as the time-independent Schrödinger equation.
More generally, this equation takes the form
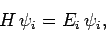 |
(296) |
where 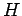 is assumed not to be an explicit function of
is assumed not to be an explicit function of 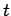 .
Of course, the
.
Of course, the 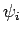 satisfy the usual orthonormality condition:
satisfy the usual orthonormality condition:
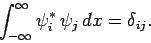 |
(297) |
Moreover, we can express a general wavefunction as a linear combination
of energy eigenstates:
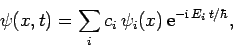 |
(298) |
where
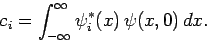 |
(299) |
Here, 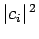 is the probability that a measurement of the energy will
yield the eigenvalue
is the probability that a measurement of the energy will
yield the eigenvalue 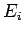 . Furthermore, immediately after such a measurement, the system is left in the corresponding energy eigenstate.
The generalization of the above results to the case where
. Furthermore, immediately after such a measurement, the system is left in the corresponding energy eigenstate.
The generalization of the above results to the case where 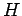 has continuous
eigenvalues is straightforward.
has continuous
eigenvalues is straightforward.
If a dynamical variable is represented by some Hermitian operator 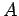 which
commutes with
which
commutes with 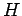 (so that it has simultaneous eigenstates with
(so that it has simultaneous eigenstates with 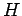 ), and
contains no specific time dependence, then it is evident from Eqs. (297) and (298) that the expectation value and
variance of
), and
contains no specific time dependence, then it is evident from Eqs. (297) and (298) that the expectation value and
variance of 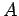 are time independent. In this sense, the dynamical
variable in question is a constant of the motion.
are time independent. In this sense, the dynamical
variable in question is a constant of the motion.
Subsections



Next: Exercises
Up: Fundamentals of Quantum Mechanics
Previous: Continuous Eigenvalues
Richard Fitzpatrick
2010-07-20
![]() which
commutes with
which
commutes with ![]() (so that it has simultaneous eigenstates with
(so that it has simultaneous eigenstates with ![]() ), and
contains no specific time dependence, then it is evident from Eqs. (297) and (298) that the expectation value and
variance of
), and
contains no specific time dependence, then it is evident from Eqs. (297) and (298) that the expectation value and
variance of ![]() are time independent. In this sense, the dynamical
variable in question is a constant of the motion.
are time independent. In this sense, the dynamical
variable in question is a constant of the motion.