Eigenvalues of
Note, from Eq. (553), that the differential operator which represents
![]() only depends on the azimuthal angle
only depends on the azimuthal angle ![]() , and is independent
of the polar angle
, and is independent
of the polar angle ![]() . It therefore follows from Eqs. (553), (556), and (570)
that
. It therefore follows from Eqs. (553), (556), and (570)
that
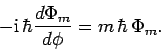 |
(573) |
Now, our basic interpretation of a wavefunction
as a quantity whose modulus squared represents the probability density
of finding a particle at a particular point in space suggests that a
physical wavefunction must be single-valued in space. Otherwise, the probability density at a given point would not, in general, have a unique value, which does not
make physical sense.
Hence, we demand that the wavefunction (574)
be single-valued: i.e.,
![]() for all
for all ![]() . This immediately implies that the quantity
. This immediately implies that the quantity ![]() is quantized.
In fact,
is quantized.
In fact, ![]() can only take integer values. Thus, we conclude that the eigenvalues
of
can only take integer values. Thus, we conclude that the eigenvalues
of ![]() are also quantized, and take the values
are also quantized, and take the values ![]() , where
, where ![]() is an integer. [A more rigorous argument is that
is an integer. [A more rigorous argument is that
![]() must be continuous in order to ensure that
must be continuous in order to ensure that ![]() is an Hermitian operator, since the proof of
hermiticity involves an integration by parts in
is an Hermitian operator, since the proof of
hermiticity involves an integration by parts in ![]() that has canceling contributions from
that has canceling contributions from ![]() and
and ![]() .]
.]
Finally, we can easily normalize the eigenstate (574) by making use of the
orthonormality constraint (572). We obtain
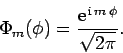 |
(575) |