

Next: Rydberg Formula
Up: Central Potentials
Previous: Infinite Spherical Potential Well
Hydrogen Atom
A hydrogen atom consists of an electron, of charge 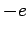 and mass
and mass 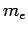 ,
and a proton, of charge
,
and a proton, of charge 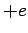 and mass
and mass 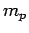 , moving in the Coulomb
potential
, moving in the Coulomb
potential
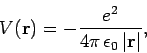 |
(661) |
where 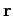 is the position vector of the electron with respect to the
proton. Now, according to the analysis in Sect. 6.4, this two-body
problem can be converted into an equivalent one-body problem. In the
latter problem, a particle of mass
is the position vector of the electron with respect to the
proton. Now, according to the analysis in Sect. 6.4, this two-body
problem can be converted into an equivalent one-body problem. In the
latter problem, a particle of mass
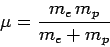 |
(662) |
moves in the central potential
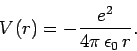 |
(663) |
Note, however, that since
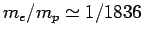 the difference
between
the difference
between 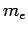 and
and 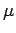 is very small. Hence, in the following,
we shall write neglect this difference entirely.
is very small. Hence, in the following,
we shall write neglect this difference entirely.
Writing the wavefunction in the usual form,
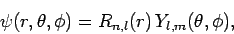 |
(664) |
it follows from Sect. 9.2 that the radial function 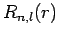 satisfies
satisfies
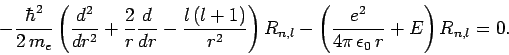 |
(665) |
Let 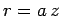 , with
, with
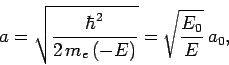 |
(666) |
where 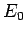 and
and 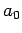 are defined in Eqs. (678) and (679),
respectively.
Here, it is assumed that
are defined in Eqs. (678) and (679),
respectively.
Here, it is assumed that 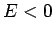 , since we are only interested in bound-states of the hydrogen atom. The above differential equation transforms
to
, since we are only interested in bound-states of the hydrogen atom. The above differential equation transforms
to
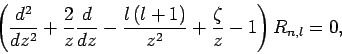 |
(667) |
where
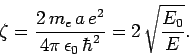 |
(668) |
Suppose that
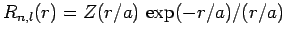 . It follows that
. It follows that
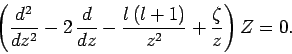 |
(669) |
We now need to solve the above differential equation in the domain 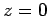 to
to 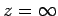 , subject to the constraint that
, subject to the constraint that 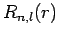 be square-integrable.
be square-integrable.
Let us look for a power-law solution of the form
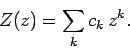 |
(670) |
Substituting this solution into Eq. (669), we obtain
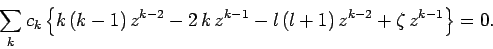 |
(671) |
Equating the coefficients of 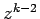 gives the recursion relation
gives the recursion relation
![\begin{displaymath}
c_k \left[k (k-1)-l (l+1)\right] = c_{k-1} \left[2 (k-1) - \zeta\right].
\end{displaymath}](img1598.png) |
(672) |
Now, the power series (670) must terminate at small 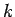 , at
some positive value of
, at
some positive value of 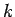 , otherwise
, otherwise 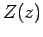 behaves unphysically as
behaves unphysically as
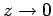 [i.e., it yields an
[i.e., it yields an 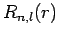 that is not square-integrable
as
that is not square-integrable
as
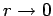 ]. From the above recursion relation, this is only possible if
]. From the above recursion relation, this is only possible if
![$[k_{min} (k_{min}-1)-l (l+1)]=0$](img1602.png) , where the first term in the series is
, where the first term in the series is
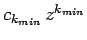 . There are two possibilities:
. There are two possibilities: 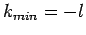 or
or 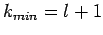 . However, the former possibility predicts unphysical behaviour of
. However, the former possibility predicts unphysical behaviour of
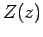 at
at 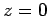 . Thus, we conclude that
. Thus, we conclude that 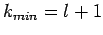 .
Note that, since
.
Note that, since
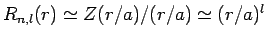 at small
at small 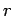 , there is a finite
probability of finding the electron at the nucleus for an
, there is a finite
probability of finding the electron at the nucleus for an 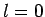 state, whereas
there is zero probability of finding the electron at the nucleus for
an
state, whereas
there is zero probability of finding the electron at the nucleus for
an 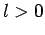 state [i.e.,
state [i.e., 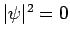 at
at 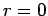 , except when
, except when
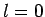 ].
].
For large values of 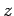 , the ratio of successive coefficients in the power series (670)
is
, the ratio of successive coefficients in the power series (670)
is
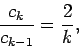 |
(673) |
according to Eq. (672). This is the same as the ratio
of successive coefficients in the power series
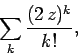 |
(674) |
which converges to 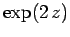 . We conclude that
. We conclude that
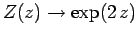 as
as
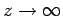 . It thus follows that
. It thus follows that
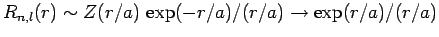 as
as
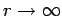 . This does not correspond to physically acceptable behaviour of the wavefunction, since
. This does not correspond to physically acceptable behaviour of the wavefunction, since
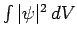 must be finite.
The only way in which we can avoid this unphysical behaviour is if the
power series (670) terminates at some maximum value of
must be finite.
The only way in which we can avoid this unphysical behaviour is if the
power series (670) terminates at some maximum value of 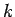 . According to
the recursion relation (672), this is only possible if
. According to
the recursion relation (672), this is only possible if
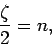 |
(675) |
where  is an integer, and the last term in the series is
is an integer, and the last term in the series is 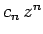 . Since the
first term in the series is
. Since the
first term in the series is
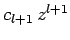 , it follows that
, it follows that  must
be greater than
must
be greater than 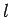 , otherwise there are no terms in the series at all.
Finally, it is clear from Eqs. (666), (668), and (675) that
, otherwise there are no terms in the series at all.
Finally, it is clear from Eqs. (666), (668), and (675) that
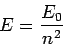 |
(676) |
and
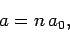 |
(677) |
where
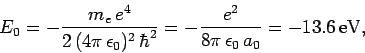 |
(678) |
and
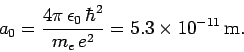 |
(679) |
Here, 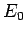 is the energy of so-called ground-state (or lowest energy state) of the
hydrogen atom, and the length
is the energy of so-called ground-state (or lowest energy state) of the
hydrogen atom, and the length 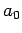 is known as the Bohr radius.
Note that
is known as the Bohr radius.
Note that
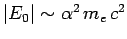 , where
, where
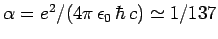 is the dimensionless fine-structure constant. The fact that
is the dimensionless fine-structure constant. The fact that
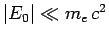 is the ultimate justification for our non-relativistic treatment of the hydrogen atom.
is the ultimate justification for our non-relativistic treatment of the hydrogen atom.
We conclude that the wavefunction of a hydrogen atom takes the form
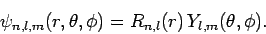 |
(680) |
Here, the
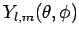 are the spherical harmonics (see Sect 8.7), and
are the spherical harmonics (see Sect 8.7), and
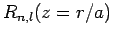 is the solution of
is the solution of
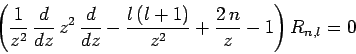 |
(681) |
which varies as 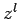 at small
at small 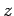 .
Furthermore, the quantum numbers
.
Furthermore, the quantum numbers  ,
, 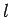 , and
, and 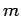 can only take values
which satisfy the inequality
can only take values
which satisfy the inequality
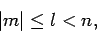 |
(682) |
where  is a positive integer,
is a positive integer, 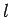 a non-negative integer, and
a non-negative integer, and 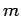 an integer.
an integer.
Now, we expect the stationary states of the hydrogen atom to be orthonormal: i.e.,
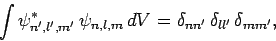 |
(683) |
where 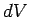 is a volume element, and the integral is over all space. Of
course,
is a volume element, and the integral is over all space. Of
course,
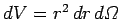 , where
, where 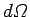 is an element
of solid angle. Moreover, we already know that the spherical
harmonics are orthonormal [see Eq. (615)]: i.e.,
is an element
of solid angle. Moreover, we already know that the spherical
harmonics are orthonormal [see Eq. (615)]: i.e.,
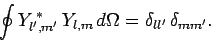 |
(684) |
It, thus, follows that the radial wavefunction satisfies the
orthonormality constraint
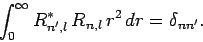 |
(685) |
The first few radial wavefunctions for the hydrogen atom are listed below:
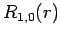 |
 |
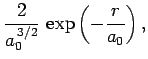 |
(686) |
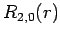 |
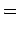 |
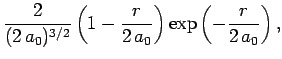 |
(687) |
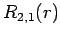 |
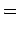 |
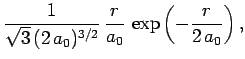 |
(688) |
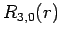 |
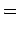 |
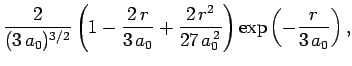 |
(689) |
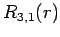 |
 |
 |
(690) |
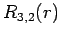 |
 |
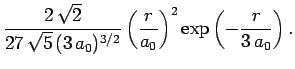 |
(691) |
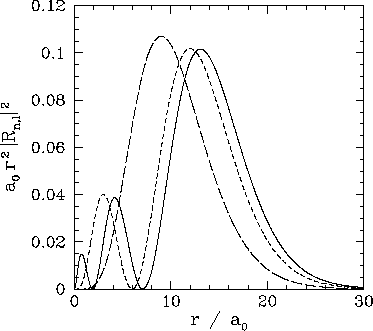
These functions are illustrated in Figs. 21 and 22.
Figure 21:
The
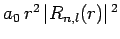 plotted as a functions of
plotted as a functions of 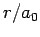 . The solid, short-dashed, and long-dashed curves correspond to
. The solid, short-dashed, and long-dashed curves correspond to
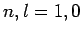 , and
, and 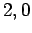 , and
, and 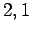 , respectively.
, respectively.
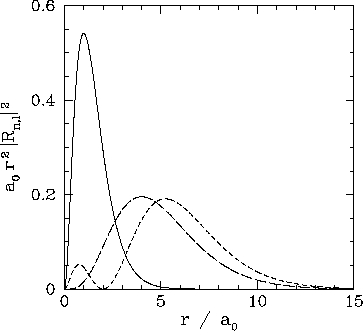 |
Figure 22:
The
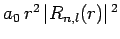 plotted as a functions of
plotted as a functions of 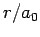 . The solid, short-dashed, and long-dashed curves correspond to
. The solid, short-dashed, and long-dashed curves correspond to
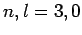 , and
, and 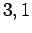 , and
, and 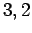 , respectively.
, respectively.
 |
Given the (properly normalized) hydrogen wavefunction (680),
plus our interpretation of 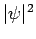 as a probability density, we can calculate
as a probability density, we can calculate
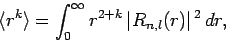 |
(692) |
where the angle-brackets denote an expectation value.
For instance, it can be demonstrated (after much tedious algebra) that
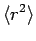 |
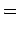 |
![$\displaystyle \frac{a_0^{ 2} n^2}{2} [5 n^2+1-3 l (l+1)],$](img1654.png) |
(693) |
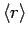 |
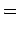 |
![$\displaystyle \frac{a_0}{2} [3 n^2-l (l+1)],$](img1656.png) |
(694) |
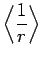 |
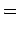 |
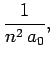 |
(695) |
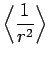 |
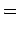 |
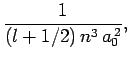 |
(696) |
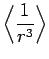 |
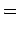 |
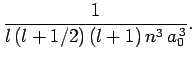 |
(697) |
According to Eq. (676), the energy levels of the bound-states of a hydrogen atom
only depend on the radial quantum number  . It turns out that this is a special
property of a
. It turns out that this is a special
property of a 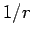 potential. For a general central potential,
potential. For a general central potential, 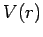 , the
quantized energy levels of a bound-state depend on both
, the
quantized energy levels of a bound-state depend on both  and
and 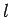 (see Sect. 9.3).
(see Sect. 9.3).
The fact that the energy levels of a hydrogen atom only depend on  ,
and not on
,
and not on 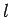 and
and 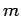 , implies that the energy spectrum of a hydrogen
atom is highly degenerate: i.e., there are many different
states which possess the same energy. According to the inequality
(682) (and the fact that
, implies that the energy spectrum of a hydrogen
atom is highly degenerate: i.e., there are many different
states which possess the same energy. According to the inequality
(682) (and the fact that  ,
, 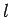 , and
, and 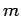 are integers), for
a given value of
are integers), for
a given value of 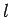 , there are
, there are 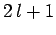 different allowed values of
different allowed values of 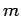 (i.e.,
(i.e.,
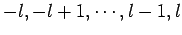 ). Likewise, for a given value of
). Likewise, for a given value of  ,
there are
,
there are  different allowed values of
different allowed values of 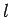 (i.e.,
(i.e.,
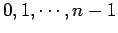 ). Now,
all states possessing the same value of
). Now,
all states possessing the same value of  have the same energy (i.e., they are degenerate). Hence, the total number of
degenerate states corresponding to a given value of
have the same energy (i.e., they are degenerate). Hence, the total number of
degenerate states corresponding to a given value of  is
is
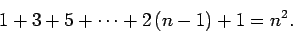 |
(698) |
Thus, the ground-state (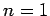 ) is not degenerate, the first excited
state (
) is not degenerate, the first excited
state (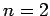 ) is four-fold degenerate, the second excited state
(
) is four-fold degenerate, the second excited state
(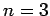 ) is nine-fold degenerate, etc. [Actually, when we take
into account the two spin states of an electron (see Sect. 10),
the degeneracy of the
) is nine-fold degenerate, etc. [Actually, when we take
into account the two spin states of an electron (see Sect. 10),
the degeneracy of the  th energy level becomes
th energy level becomes 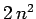 .]
.]


Next: Rydberg Formula
Up: Central Potentials
Previous: Infinite Spherical Potential Well
Richard Fitzpatrick
2010-07-20
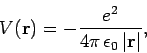
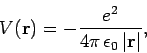
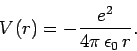
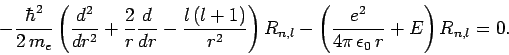
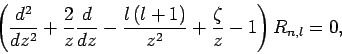
![]() , the ratio of successive coefficients in the power series (670)
is
, the ratio of successive coefficients in the power series (670)
is
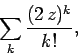
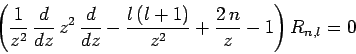
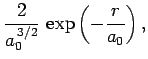
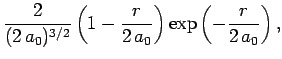
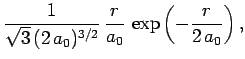
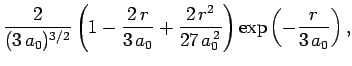
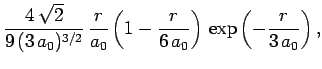
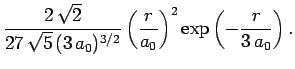


![]() as a probability density, we can calculate
as a probability density, we can calculate
![]() . It turns out that this is a special
property of a
. It turns out that this is a special
property of a ![]() potential. For a general central potential,
potential. For a general central potential, ![]() , the
quantized energy levels of a bound-state depend on both
, the
quantized energy levels of a bound-state depend on both ![]() and
and ![]() (see Sect. 9.3).
(see Sect. 9.3).
![]() ,
and not on
,
and not on ![]() and
and ![]() , implies that the energy spectrum of a hydrogen
atom is highly degenerate: i.e., there are many different
states which possess the same energy. According to the inequality
(682) (and the fact that
, implies that the energy spectrum of a hydrogen
atom is highly degenerate: i.e., there are many different
states which possess the same energy. According to the inequality
(682) (and the fact that ![]() ,
, ![]() , and
, and ![]() are integers), for
a given value of
are integers), for
a given value of ![]() , there are
, there are ![]() different allowed values of
different allowed values of ![]() (i.e.,
(i.e.,
![]() ). Likewise, for a given value of
). Likewise, for a given value of ![]() ,
there are
,
there are ![]() different allowed values of
different allowed values of ![]() (i.e.,
(i.e.,
![]() ). Now,
all states possessing the same value of
). Now,
all states possessing the same value of ![]() have the same energy (i.e., they are degenerate). Hence, the total number of
degenerate states corresponding to a given value of
have the same energy (i.e., they are degenerate). Hence, the total number of
degenerate states corresponding to a given value of ![]() is
is