


Next: Angular Momentum in the
Up: Addition of Angular Momentum
Previous: Introduction
General Principles
The three basic orbital angular momentum operators, 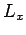 ,
, 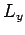 ,
and
,
and  , obey the commutation relations (531)-(533),
which can be written in the convenient vector form:
, obey the commutation relations (531)-(533),
which can be written in the convenient vector form:
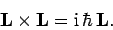 |
(779) |
Likewise, the three basic spin angular momentum operators, 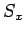 ,
, 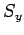 ,
and
,
and  , obey the commutation relations (702)-(704),
which can also be written in vector form: i.e.,
, obey the commutation relations (702)-(704),
which can also be written in vector form: i.e.,
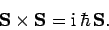 |
(780) |
Now, since the orbital angular momentum operators are associated
with the electron's motion through space, whilst the spin angular
momentum operators are associated with its internal
motion, and these two types of motion are completely unrelated (i.e., they correspond to different degrees of freedom--see Sect. 6.2), it is reasonable to suppose that the two sets of operators commute with
one another: i.e.,
![\begin{displaymath}[L_i, S_j]= 0,
\end{displaymath}](img1869.png) |
(781) |
where 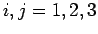 corresponds to
corresponds to 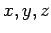 .
.
Let us now consider the electron's total angular momentum vector
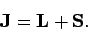 |
(782) |
We have
In other words,
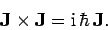 |
(784) |
It is thus evident that the three basic total angular momentum operators, 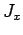 ,
,
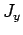 , and
, and 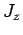 , obey analogous commutation relations to the
corresponding orbital and spin angular momentum operators. It therefore follows
that the total angular momentum has similar properties to the
orbital and spin angular momenta. For instance, it is
only possible to simultaneously measure the magnitude
squared of the total angular momentum vector,
, obey analogous commutation relations to the
corresponding orbital and spin angular momentum operators. It therefore follows
that the total angular momentum has similar properties to the
orbital and spin angular momenta. For instance, it is
only possible to simultaneously measure the magnitude
squared of the total angular momentum vector,
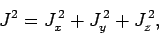 |
(785) |
together with a single Cartesian component. By convention, we shall
always choose to measure 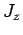 . A simultaneous eigenstate
of
. A simultaneous eigenstate
of 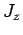 and
and 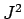 satisfies
satisfies
where the quantum number 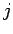 can take positive integer, or half-integer,
values, and the quantum number
can take positive integer, or half-integer,
values, and the quantum number 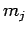 is restricted to the following
range of values:
is restricted to the following
range of values:
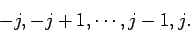 |
(788) |
Now
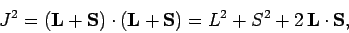 |
(789) |
which can also be written as
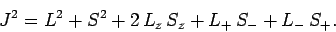 |
(790) |
We know that the operator 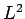 commutes with itself, with all of the
Cartesian components of
commutes with itself, with all of the
Cartesian components of 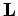 (and, hence, with the raising
and lowering operators
(and, hence, with the raising
and lowering operators 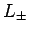 ), and with all of the spin angular momentum
operators (see Sect. 8.2). It is therefore clear that
), and with all of the spin angular momentum
operators (see Sect. 8.2). It is therefore clear that
![\begin{displaymath}[J^2,L^2]= 0.
\end{displaymath}](img1892.png) |
(791) |
A similar argument allows us to also conclude that
![\begin{displaymath}[J^2,S^2]=0.
\end{displaymath}](img1893.png) |
(792) |
Now, the operator  commutes with itself, with
commutes with itself, with 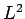 , with all of
the spin angular momentum operators, but not with the raising
and lowering operators
, with all of
the spin angular momentum operators, but not with the raising
and lowering operators 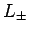 (see Sect. 8.2). It follows that
(see Sect. 8.2). It follows that
![\begin{displaymath}[J^2,L_z]\neq 0.
\end{displaymath}](img1894.png) |
(793) |
Likewise, we can also show that
![\begin{displaymath}[J^2,S_z]\neq 0.
\end{displaymath}](img1895.png) |
(794) |
Finally, we have
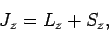 |
(795) |
where
![$[J_z,L_z]=[J_z,S_z]=0$](img1897.png) .
.
Recalling that only commuting operators correspond to physical
quantities which can be simultaneously measured (see Sect. 4.10),
it follows, from the above discussion, that there are two alternative sets of
physical variables associated with angular momentum which we can measure simultaneously.
The first set correspond to the operators 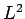 ,
, 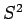 ,
,  ,
,  , and
, and 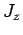 . The second set correspond to the operators
. The second set correspond to the operators
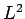 ,
, 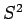 ,
, 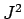 , and
, and 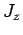 . In other words, we can always measure
the magnitude squared of the orbital and spin angular momentum vectors, together with
the
. In other words, we can always measure
the magnitude squared of the orbital and spin angular momentum vectors, together with
the 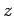 -component of the total angular momentum vector.
In addition, we can either choose to measure the
-component of the total angular momentum vector.
In addition, we can either choose to measure the 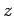 -components of
the orbital and spin angular momentum vectors, or the magnitude squared
of the total angular momentum vector.
-components of
the orbital and spin angular momentum vectors, or the magnitude squared
of the total angular momentum vector.
Let
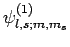 represent a simultaneous eigenstate
of
represent a simultaneous eigenstate
of 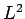 ,
, 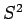 ,
,  , and
, and  corresponding to the following
eigenvalues:
corresponding to the following
eigenvalues:
It is easily seen that
Hence,
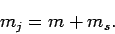 |
(801) |
In other words, the quantum numbers controlling the 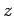 -components
of the various angular momentum vectors can simply be added algebraically.
-components
of the various angular momentum vectors can simply be added algebraically.
Finally, let
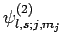 represent a simultaneous eigenstate
of
represent a simultaneous eigenstate
of 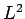 ,
, 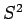 ,
, 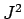 , and
, and 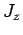 corresponding to the following
eigenvalues:
corresponding to the following
eigenvalues:



Next: Angular Momentum in the
Up: Addition of Angular Momentum
Previous: Introduction
Richard Fitzpatrick
2010-07-20
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The second set correspond to the operators
. The second set correspond to the operators
![]() ,
, ![]() ,
, ![]() , and
, and ![]() . In other words, we can always measure
the magnitude squared of the orbital and spin angular momentum vectors, together with
the
. In other words, we can always measure
the magnitude squared of the orbital and spin angular momentum vectors, together with
the ![]() -component of the total angular momentum vector.
In addition, we can either choose to measure the
-component of the total angular momentum vector.
In addition, we can either choose to measure the ![]() -components of
the orbital and spin angular momentum vectors, or the magnitude squared
of the total angular momentum vector.
-components of
the orbital and spin angular momentum vectors, or the magnitude squared
of the total angular momentum vector.
![]() represent a simultaneous eigenstate
of
represent a simultaneous eigenstate
of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() corresponding to the following
eigenvalues:
corresponding to the following
eigenvalues:
![]() represent a simultaneous eigenstate
of
represent a simultaneous eigenstate
of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() corresponding to the following
eigenvalues:
corresponding to the following
eigenvalues: