

Next: Time-Independent Perturbation Theory
Up: Two Spin One-Half Particles
Previous: Two Spin One-Half Particles
- An electron in a hydrogen atom occupies the combined spin
and position state
- What values would a measurement of
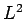 yield, and with
what probabilities?
yield, and with
what probabilities?
- Same for
 .
.
- Same for
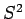 .
.
- Same for
 .
.
- Same for
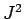 .
.
- Same for
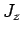 .
.
- What is the probability density for finding the electron at
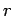 ,
, 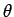 ,
, 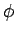 ?
?
- What is the probability density for finding the electron in the
spin up state (with respect to the
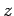 -axis) at radius
-axis) at radius 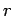 ?
?
- In a low energy neutron-proton system (with zero orbital angular
momentum) the potential energy is given by
where
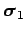 denotes the vector of the Pauli matrices of the neutron,
and
denotes the vector of the Pauli matrices of the neutron,
and
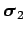 denotes the vector of the Pauli matrices of the proton. Calculate
the potential energy for the neutron-proton system:
denotes the vector of the Pauli matrices of the proton. Calculate
the potential energy for the neutron-proton system:
- In the spin singlet state.
- In the spin triplet state.
- Consider two electrons in a spin singlet state.
- If a measurement of the spin of one of the electrons shows that it
is in the state with
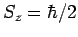 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the 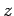 -component of the spin of the
other electron yields
-component of the spin of the
other electron yields 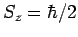 ?
?
- If a measurement of the spin of one of the electrons shows
that it is in the state with
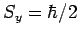 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the 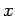 -component of the spin of the
other electron yields
-component of the spin of the
other electron yields 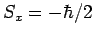 ?
?
Finally, if electron 1 is in a spin state described by
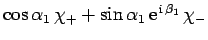 , and
electron 2 is in a spin state described by
, and
electron 2 is in a spin state described by
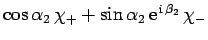 , what is
the probability that the two-electron spin state is a triplet state?
, what is
the probability that the two-electron spin state is a triplet state?


Next: Time-Independent Perturbation Theory
Up: Two Spin One-Half Particles
Previous: Two Spin One-Half Particles
Richard Fitzpatrick
2010-07-20
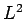 yield, and with
what probabilities?
yield, and with
what probabilities?
 .
.
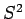 .
.
 .
.
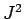 .
.
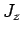 .
.
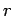 ,
, 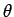 ,
, 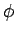 ?
?
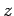 -axis) at radius
-axis) at radius 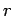 ?
?
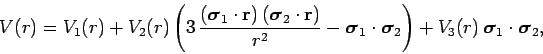
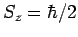 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the 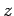 -component of the spin of the
other electron yields
-component of the spin of the
other electron yields 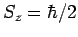 ?
?
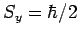 , what is the probability that a
measurement of the
, what is the probability that a
measurement of the 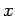 -component of the spin of the
other electron yields
-component of the spin of the
other electron yields 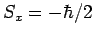 ?
?