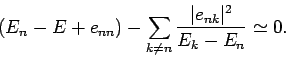

Next: Quadratic Stark Effect
Up: Time-Independent Perturbation Theory
Previous: Two-State System
Non-Degenerate Perturbation Theory
Let us now generalize our perturbation analysis to deal
with systems possessing more than two energy eigenstates.
Consider a system in which the energy
eigenstates of the unperturbed Hamiltonian, 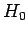 , are denoted
, are denoted
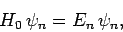 |
(894) |
where  runs from 1 to
runs from 1 to 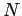 . The eigenstates are assumed to
be orthonormal, so that
. The eigenstates are assumed to
be orthonormal, so that
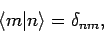 |
(895) |
and to form a complete set. Let us now try to
solve the energy eigenvalue problem for the perturbed Hamiltonian:
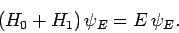 |
(896) |
If follows that
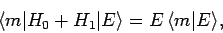 |
(897) |
where 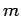 can take any value from 1 to
can take any value from 1 to 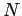 . Now, we can express
. Now, we can express
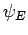 as a linear superposition of the unperturbed energy eigenstates:
as a linear superposition of the unperturbed energy eigenstates:
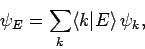 |
(898) |
where 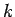 runs from 1 to
runs from 1 to 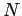 . We can combine the above
equations to give
. We can combine the above
equations to give
 |
(899) |
where
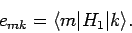 |
(900) |
Let us now develop our perturbation expansion. We assume that
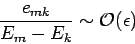 |
(901) |
for all 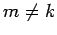 , where
, where 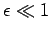 is our expansion parameter.
We also assume that
is our expansion parameter.
We also assume that
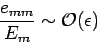 |
(902) |
for all 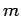 . Let us search for a modified version of the
. Let us search for a modified version of the  th unperturbed
energy eigenstate for which
th unperturbed
energy eigenstate for which
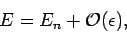 |
(903) |
and
for 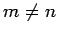 . Suppose that we write out Eq. (899) for
. Suppose that we write out Eq. (899) for 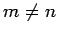 ,
neglecting terms which are
,
neglecting terms which are
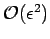 according to our expansion
scheme. We find that
according to our expansion
scheme. We find that
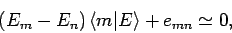 |
(906) |
giving
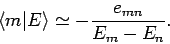 |
(907) |
Substituting the above expression into Eq. (899),
evaluated for 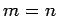 , and neglecting
, and neglecting
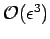 terms, we obtain
terms, we obtain
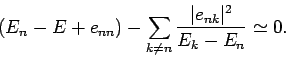 |
(908) |
Thus, the modified  th energy eigenstate possesses an eigenvalue
th energy eigenstate possesses an eigenvalue
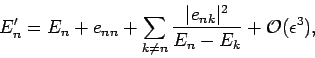 |
(909) |
and a wavefunction
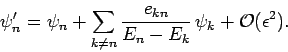 |
(910) |
Incidentally, it is easily demonstrated that the modified eigenstates remain orthonormal
to
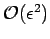 .
.


Next: Quadratic Stark Effect
Up: Time-Independent Perturbation Theory
Previous: Two-State System
Richard Fitzpatrick
2010-07-20