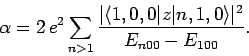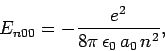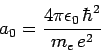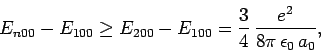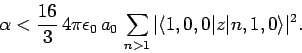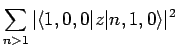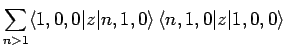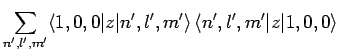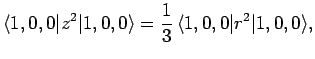

Next: Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Non-Degenerate Perturbation Theory
Quadratic Stark Effect
Suppose that a hydrogen atom is
subject to a uniform external electric field, of magnitude 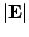 , directed along the
, directed along the 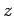 -axis. The Hamiltonian of the system can be split into two parts. Namely, the unperturbed
Hamiltonian,
-axis. The Hamiltonian of the system can be split into two parts. Namely, the unperturbed
Hamiltonian,
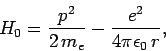 |
(911) |
and the perturbing Hamiltonian
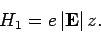 |
(912) |
Note that the electron spin is irrelevant to this problem
(since the spin operators all commute with 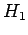 ), so we can ignore
the spin degrees of freedom of the system. Hence, the energy eigenstates
of the unperturbed Hamiltonian are characterized by three quantum
numbers--the radial quantum number
), so we can ignore
the spin degrees of freedom of the system. Hence, the energy eigenstates
of the unperturbed Hamiltonian are characterized by three quantum
numbers--the radial quantum number 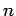 , and the two angular
quantum numbers
, and the two angular
quantum numbers 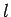 and
and 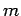 (see Cha. 9). Let us
denote these states as the
(see Cha. 9). Let us
denote these states as the 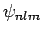 , and let their corresponding energy eigenvalues
be the
, and let their corresponding energy eigenvalues
be the 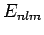 . According to the analysis in the previous section, the change in energy of the eigenstate characterized by the quantum
numbers
. According to the analysis in the previous section, the change in energy of the eigenstate characterized by the quantum
numbers 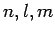 in the presence of a small electric field is given by
in the presence of a small electric field is given by
This energy-shift is known as the Stark effect.
The sum on the right-hand side of the above equation seems very complicated. However, it turns out that most of the terms in this sum
are zero. This follows because the matrix elements
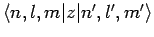 are zero for virtually all choices of the two sets of quantum number,
are zero for virtually all choices of the two sets of quantum number, 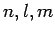 and
and
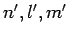 . Let us try to find a set of rules which determine when these
matrix elements are non-zero. These rules are usually referred to as the
selection rules for the problem in hand.
. Let us try to find a set of rules which determine when these
matrix elements are non-zero. These rules are usually referred to as the
selection rules for the problem in hand.
Now, since [see Eq. (529)]
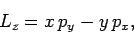 |
(914) |
it follows that [see Eqs. (481)-(483)]
![\begin{displaymath}[L_z,z]= 0.
\end{displaymath}](img2183.png) |
(915) |
Thus,
since 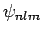 is, by definition, an eigenstate of
is, by definition, an eigenstate of  corresponding
to the eigenvalue
corresponding
to the eigenvalue 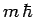 . Hence, it is clear, from the above equation,
that one of the selection rules is that the matrix element
. Hence, it is clear, from the above equation,
that one of the selection rules is that the matrix element
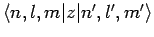 is zero unless
is zero unless
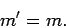 |
(917) |
Let us now determine the selection rule for 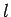 . We have
. We have
where use has been made of Eqs. (481)-(483), (527)-(529), and (535).
Thus,
which reduces to
However, it is clear from Eqs. (527)-(529) that
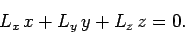 |
(921) |
Hence, we obtain
![\begin{displaymath}[L^2,[L^2,z]] = 2 \hbar^2 (L^2 z+z L^2).
\end{displaymath}](img2203.png) |
(922) |
Finally, the above expression expands to give
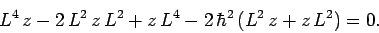 |
(923) |
Equation (923) implies that
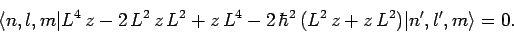 |
(924) |
Since, by definition, 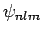 is an eigenstate of
is an eigenstate of 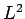 corresponding
to the eigenvalue
corresponding
to the eigenvalue
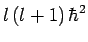 , this expression yields
, this expression yields
which reduces to
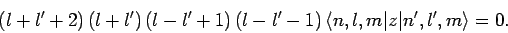 |
(926) |
According to the above formula, the matrix element
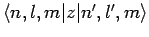 vanishes unless
vanishes unless 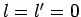 or
or 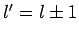 . [Of course, the
factor
. [Of course, the
factor 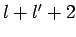 , in the above equation, can never be zero, since
, in the above equation, can never be zero, since 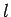 and
and 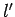 can never be negative.]
Recall, however, from Cha. 9, that an
can never be negative.]
Recall, however, from Cha. 9, that an 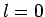 wavefunction
is spherically symmetric. It, therefore, follows, from symmetry,
that the matrix element
wavefunction
is spherically symmetric. It, therefore, follows, from symmetry,
that the matrix element
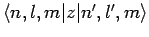 is zero when
is zero when
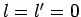 . In conclusion, the selection rule for
. In conclusion, the selection rule for 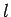 is that the
matrix element
is that the
matrix element
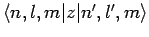 is zero unless
is zero unless
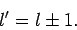 |
(927) |
Application of the selection rules (917) and (927) to
Eq. (913) yields
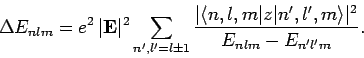 |
(928) |
Note that, according to the selection rules, all of the terms in Eq. (913) which vary linearly with
the electric field-strength vanish.
Only those terms which vary quadratically with the field-strength
survive. Hence, this type of energy-shift of an atomic state in the
presence of a small electric field is known as the quadratic
Stark effect. Now, the electric polarizability of an atom is
defined in terms of the energy-shift of the atomic state as follows:
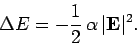 |
(929) |
Hence, we can write
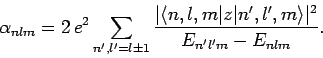 |
(930) |
Unfortunately, there is one fairly obvious problem with Eq. (928). Namely, it predicts an infinite energy-shift if there exists some non-zero
matrix element
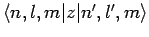 which couples
two degenerate unperturbed energy eigenstates: i.e.,
if
which couples
two degenerate unperturbed energy eigenstates: i.e.,
if
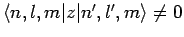 and
and
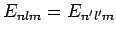 .
Clearly, our perturbation method breaks down completely in this
situation. Hence, we conclude that Eqs. (928) and (930)
are only applicable to cases where the coupled eigenstates are
non-degenerate. For this reason, the type of perturbation
theory employed here is known as non-degenerate perturbation theory.
Now, the unperturbed eigenstates of a hydrogen atom have energies which
only depend on the radial quantum number
.
Clearly, our perturbation method breaks down completely in this
situation. Hence, we conclude that Eqs. (928) and (930)
are only applicable to cases where the coupled eigenstates are
non-degenerate. For this reason, the type of perturbation
theory employed here is known as non-degenerate perturbation theory.
Now, the unperturbed eigenstates of a hydrogen atom have energies which
only depend on the radial quantum number 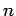 (see Cha. 9). It follows that
we can only apply the above results to the
(see Cha. 9). It follows that
we can only apply the above results to the 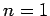 eigenstate (since
for
eigenstate (since
for 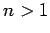 there will be coupling to degenerate eigenstates with
the same value of
there will be coupling to degenerate eigenstates with
the same value of 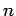 but different values of
but different values of 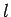 ).
).
Thus, according to non-degenerate perturbation theory, the polarizability of the ground-state (i.e., 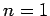 ) of a hydrogen atom is given by
) of a hydrogen atom is given by
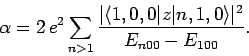 |
(931) |
Here, we have made use of the fact that
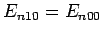 . The sum in the above expression can be
evaluated approximately by noting that (see Sect. 9.4)
. The sum in the above expression can be
evaluated approximately by noting that (see Sect. 9.4)
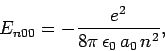 |
(932) |
where
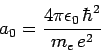 |
(933) |
is the Bohr radius. Hence, we can write
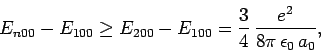 |
(934) |
which implies that
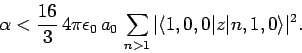 |
(935) |
However, [see Eq. (874)]
where we have made use of the selection rules, the fact that the
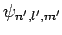 form a complete set, and the fact the the
ground-state of hydrogen is spherically symmetric. Finally, it
follows from Eq. (693) that
form a complete set, and the fact the the
ground-state of hydrogen is spherically symmetric. Finally, it
follows from Eq. (693) that
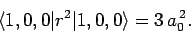 |
(937) |
Hence, we conclude that
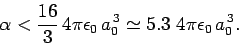 |
(938) |
The exact result (which can be obtained by solving Schrödinger's equation
in parabolic coordinates) is
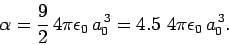 |
(939) |


Next: Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Non-Degenerate Perturbation Theory
Richard Fitzpatrick
2010-07-20
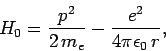
![]() ), so we can ignore
the spin degrees of freedom of the system. Hence, the energy eigenstates
of the unperturbed Hamiltonian are characterized by three quantum
numbers--the radial quantum number
), so we can ignore
the spin degrees of freedom of the system. Hence, the energy eigenstates
of the unperturbed Hamiltonian are characterized by three quantum
numbers--the radial quantum number ![]() , and the two angular
quantum numbers
, and the two angular
quantum numbers ![]() and
and ![]() (see Cha. 9). Let us
denote these states as the
(see Cha. 9). Let us
denote these states as the ![]() , and let their corresponding energy eigenvalues
be the
, and let their corresponding energy eigenvalues
be the ![]() . According to the analysis in the previous section, the change in energy of the eigenstate characterized by the quantum
numbers
. According to the analysis in the previous section, the change in energy of the eigenstate characterized by the quantum
numbers ![]() in the presence of a small electric field is given by
in the presence of a small electric field is given by
![]() are zero for virtually all choices of the two sets of quantum number,
are zero for virtually all choices of the two sets of quantum number, ![]() and
and
![]() . Let us try to find a set of rules which determine when these
matrix elements are non-zero. These rules are usually referred to as the
selection rules for the problem in hand.
. Let us try to find a set of rules which determine when these
matrix elements are non-zero. These rules are usually referred to as the
selection rules for the problem in hand.
![]() . We have
. We have
![]() which couples
two degenerate unperturbed energy eigenstates: i.e.,
if
which couples
two degenerate unperturbed energy eigenstates: i.e.,
if
![]() and
and
![]() .
Clearly, our perturbation method breaks down completely in this
situation. Hence, we conclude that Eqs. (928) and (930)
are only applicable to cases where the coupled eigenstates are
non-degenerate. For this reason, the type of perturbation
theory employed here is known as non-degenerate perturbation theory.
Now, the unperturbed eigenstates of a hydrogen atom have energies which
only depend on the radial quantum number
.
Clearly, our perturbation method breaks down completely in this
situation. Hence, we conclude that Eqs. (928) and (930)
are only applicable to cases where the coupled eigenstates are
non-degenerate. For this reason, the type of perturbation
theory employed here is known as non-degenerate perturbation theory.
Now, the unperturbed eigenstates of a hydrogen atom have energies which
only depend on the radial quantum number ![]() (see Cha. 9). It follows that
we can only apply the above results to the
(see Cha. 9). It follows that
we can only apply the above results to the ![]() eigenstate (since
for
eigenstate (since
for ![]() there will be coupling to degenerate eigenstates with
the same value of
there will be coupling to degenerate eigenstates with
the same value of ![]() but different values of
but different values of ![]() ).
).
![]() ) of a hydrogen atom is given by
) of a hydrogen atom is given by