

Next: Variational Methods
Up: Time-Dependent Perturbation Theory
Previous: Intensity Rules
Atomic transitions which are forbidden by the electric dipole selection rules (1149)
and (1150) are unsurprisingly known as forbidden transitions.
It is clear from the analysis in Sect. 13.8 that a forbidden
transition is one for which the matrix element
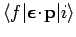 is zero. However, this matrix element is only an approximation
to the true matrix element for radiative transitions, which
takes the form
is zero. However, this matrix element is only an approximation
to the true matrix element for radiative transitions, which
takes the form
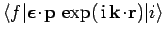 . Expanding
. Expanding
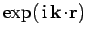 ,
and keeping the first two terms, the matrix element for a forbidden
transition becomes
,
and keeping the first two terms, the matrix element for a forbidden
transition becomes
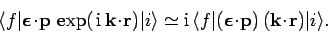 |
(1164) |
Hence, if the residual matrix element on the right-hand side of the above expression
is non-zero then a ``forbidden'' transition can take place, allbeit at
a much reduced rate. In fact, in Sect. 13.9, we calculated that the
typical rate of an electric dipole transition is
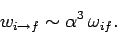 |
(1165) |
Since the transition rate is proportional to the square of the radiative matrix element, it is clear that the transition rate for a forbidden
transition enabled by the residual matrix element (1164) is smaller than that of an electric dipole transition by
a factor 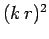 . Estimating
. Estimating 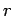 as the Bohr radius, and
as the Bohr radius, and 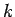 as the wavenumber of a typical spectral line of hydrogen, it is
easily demonstrated that
as the wavenumber of a typical spectral line of hydrogen, it is
easily demonstrated that
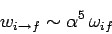 |
(1166) |
for such a transition.
Of course, there are some transitions (in particular, the
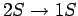 transition) for which the true radiative matrix element
transition) for which the true radiative matrix element
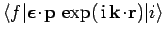 is
zero. Such transitions are absolutely forbidden.
is
zero. Such transitions are absolutely forbidden.
Finally, it is fairly obvious that excited states which decay via forbidden transitions
have much longer life-times than those which decay
via electric dipole transitions. Since the natural width of a spectral line
is inversely proportional to the life-time of the associated decaying state, it follows
that spectral lines associated with forbidden transitions are generally much sharper than those
associated with electric dipole transitions.


Next: Variational Methods
Up: Time-Dependent Perturbation Theory
Previous: Intensity Rules
Richard Fitzpatrick
2010-07-20