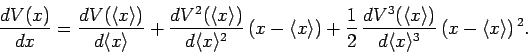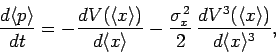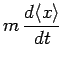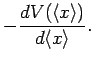

Next: Operators
Up: Fundamentals of Quantum Mechanics
Previous: Expectation Values and Variances
Ehrenfest's Theorem
A simple way to calculate the expectation value of
momentum
is to evaluate the time derivative of
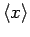 , and then
multiply by the mass
, and then
multiply by the mass 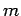 : i.e.,
: i.e.,
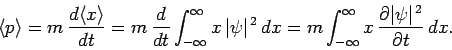 |
(170) |
However, it is easily demonstrated that
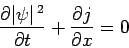 |
(171) |
[this is just the differential form of Eq. (154)],
where 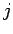 is the probability current defined in Eq. (155).
Thus,
is the probability current defined in Eq. (155).
Thus,
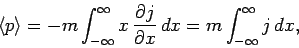 |
(172) |
where we have integrated by parts. It follows from Eq. (155)
that
 |
(173) |
where we have again integrated by parts. Hence, the expectation value of the momentum can be written
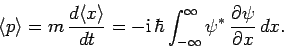 |
(174) |
It follows from the above that
where we have integrated by parts.
Substituting from Schrödinger's equation (137), and simplifying, we obtain
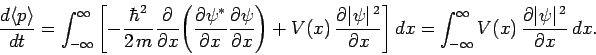 |
(176) |
Integration by parts yields
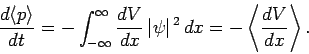 |
(177) |
Hence, according to Eqs. (170) and (177),
Evidently, the expectation values of displacement and momentum obey
time evolution equations which are analogous to those of classical mechanics.
This result is known as Ehrenfest's theorem.
Suppose that the potential 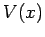 is slowly varying. In this case, we can
expand
is slowly varying. In this case, we can
expand 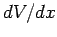 as a Taylor series about
as a Taylor series about
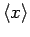 . Keeping
terms up to second order, we obtain
. Keeping
terms up to second order, we obtain
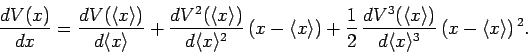 |
(180) |
Substitution of the above expansion into Eq. (179) yields
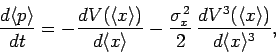 |
(181) |
since
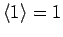 , and
, and
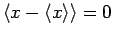 ,
and
,
and
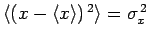 .
The final term on the right-hand side of the above equation can be neglected
when the spatial extent of the particle wavefunction,
.
The final term on the right-hand side of the above equation can be neglected
when the spatial extent of the particle wavefunction, 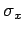 , is much
smaller than the variation length-scale of the potential. In this case,
Eqs. (178) and (179) reduce to
, is much
smaller than the variation length-scale of the potential. In this case,
Eqs. (178) and (179) reduce to
These equations are exactly equivalent to the equations of classical
mechanics, with
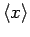 playing the role of the particle displacement. Of course, if the spatial extent of the wavefunction is negligible
then a measurement of
playing the role of the particle displacement. Of course, if the spatial extent of the wavefunction is negligible
then a measurement of 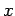 is almost certain to yield a result which lies
very close to
is almost certain to yield a result which lies
very close to
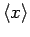 . Hence, we conclude that quantum mechanics
corresponds to classical mechanics in the limit that the spatial
extent of the wavefunction (which is typically of order the de Boglie wavelength) is negligible. This is an important result, since we know that
classical mechanics gives the correct answer in this limit.
. Hence, we conclude that quantum mechanics
corresponds to classical mechanics in the limit that the spatial
extent of the wavefunction (which is typically of order the de Boglie wavelength) is negligible. This is an important result, since we know that
classical mechanics gives the correct answer in this limit.


Next: Operators
Up: Fundamentals of Quantum Mechanics
Previous: Expectation Values and Variances
Richard Fitzpatrick
2010-07-20
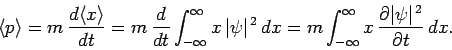
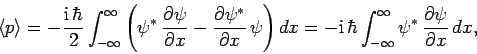
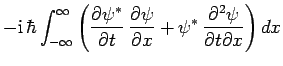
![$\displaystyle \int_{-\infty}^{\infty}\left[ \left({\rm i} \hbar \frac{\partia...
...artial x}\left({\rm i} \hbar \frac{\partial\psi}{\partial t}\right)\right]dx,$](img511.png)
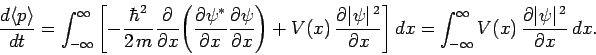
![]() is slowly varying. In this case, we can
expand
is slowly varying. In this case, we can
expand ![]() as a Taylor series about
as a Taylor series about
![]() . Keeping
terms up to second order, we obtain
. Keeping
terms up to second order, we obtain