| (516) |
A burnt-out star is basically a gas of electrons and ions. As the star collapses, its density increases, and so the mean separation between its constituent particles decreases. Eventually, the mean separation becomes of order the de Broglie wavelength of the electrons, and the electron gas becomes degenerate. Note, that the de Broglie wavelength of the ions is much smaller than that of the electrons, so the ion gas remains non-degenerate. Now, even at zero temperature, a degenerate electron gas exerts a substantial pressure, because the Pauli exclusion principle prevents the mean electron separation from becoming significantly smaller than the typical de Broglie wavelength (see previous section). Thus, it is possible for a burnt-out star to maintain itself against complete collapse under gravity via the degeneracy pressure of its constituent electrons. Such stars are termed white-dwarfs. Let us investigate the physics of white-dwarfs in more detail.
The total energy of a white-dwarf star can be written
From the previous subsection, the kinetic energy of a degenerate electron gas is simply
The interior of a white-dwarf star is composed of atoms like
![]() and
and ![]() which contain equal numbers of protons, neutrons, and
electrons. Thus,
which contain equal numbers of protons, neutrons, and
electrons. Thus,
Equations (516)-(519) can be combined to give
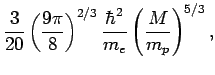 |
(521) | ||
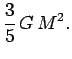 |
(522) |
| (523) |
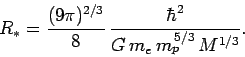 |
(524) |
Note from Eqs. (518), (519), and (525)
that
![]() . In other words, the mean energy of the
electrons inside a white dwarf increases as the stellar mass increases.
Hence, for a sufficiently massive white dwarf, the electrons can become
relativistic. It turns out that the degeneracy pressure for
relativistic electrons only scales as
. In other words, the mean energy of the
electrons inside a white dwarf increases as the stellar mass increases.
Hence, for a sufficiently massive white dwarf, the electrons can become
relativistic. It turns out that the degeneracy pressure for
relativistic electrons only scales as ![]() , rather that
, rather that ![]() ,
and thus is unable to balance the gravitational pressure [which also
scales as
,
and thus is unable to balance the gravitational pressure [which also
scales as ![]() --see Eq. (520)]. It follows that electron
degeneracy pressure is only able to halt the collapse of a burnt-out star
provided that the stellar mass does not exceed some critical value, known
as the Chandrasekhar limit,
which turns out to be about
--see Eq. (520)]. It follows that electron
degeneracy pressure is only able to halt the collapse of a burnt-out star
provided that the stellar mass does not exceed some critical value, known
as the Chandrasekhar limit,
which turns out to be about ![]() times the mass of the Sun. Stars
whose mass exceeds the Chandrasekhar limit inevitably collapse to
produce extremely compact objects, such as neutron stars (which are
held up by the degeneracy pressure of their constituent neutrons),
or black holes.
times the mass of the Sun. Stars
whose mass exceeds the Chandrasekhar limit inevitably collapse to
produce extremely compact objects, such as neutron stars (which are
held up by the degeneracy pressure of their constituent neutrons),
or black holes.