![\begin{displaymath}
V(x) = \left\{\begin{array}{lcl}
V_0&\mbox{\hspace{1cm}}&\mb...
...eq x\leq a$}\ [0.5ex]
0&&\mbox{otherwise}
\end{array}\right.,
\end{displaymath}](img812.png) |
(313) |
![\begin{displaymath}
V(x) = \left\{\begin{array}{lcl}
V_0&\mbox{\hspace{1cm}}&\mb...
...eq x\leq a$}\ [0.5ex]
0&&\mbox{otherwise}
\end{array}\right.,
\end{displaymath}](img812.png) |
(313) |
Let us adopt the following solution
of the above equation to the left of the barrier (i.e., ![]() ):
):
| (315) |
| (316) |
Let us adopt the following solution to Eq. (314) to the right
of the barrier (i.e. ![]() ):
):
| (317) |
| (318) |
Inside the barrier (i.e.,
![]() ),
), ![]() satisfies
satisfies
| (321) |
Let us, first of all, consider the case where ![]() . In this case, the general
solution to Eq. (320) inside the barrier takes the
form
. In this case, the general
solution to Eq. (320) inside the barrier takes the
form
| (322) |
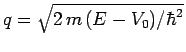 .
.
Now, the boundary conditions at the edges of the barrier (i.e., at
![]() and
and ![]() ) are that
) are that ![]() and
and ![]() are both
continuous. These boundary conditions ensure that the probability current
(155) remains finite and continuous across the edges of the boundary, as must be the
case if it is to be a spatial constant.
are both
continuous. These boundary conditions ensure that the probability current
(155) remains finite and continuous across the edges of the boundary, as must be the
case if it is to be a spatial constant.
Continuity of ![]() and
and ![]() at the left edge of
the barrier (i.e.,
at the left edge of
the barrier (i.e., ![]() ) yields
) yields
| (323) | |||
| (324) |
| (325) | |||
| (326) |
It is instructive to compare the quantum mechanical probabilities
of reflection and transmission--(327) and (328), respectively--with those derived from classical physics. Now, according
to classical physics, if a particle of energy ![]() is incident on
a potential barrier of height
is incident on
a potential barrier of height ![]() then the particle slows down
as it passes through the barrier, but is otherwise unaffected.
In other words, the classical probability of reflection is
zero, and the classical probability of transmission is unity.
then the particle slows down
as it passes through the barrier, but is otherwise unaffected.
In other words, the classical probability of reflection is
zero, and the classical probability of transmission is unity.
 |
 |
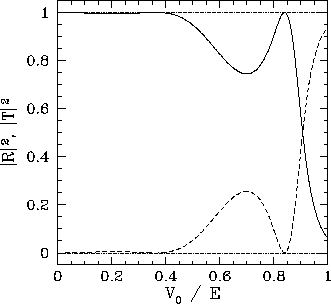
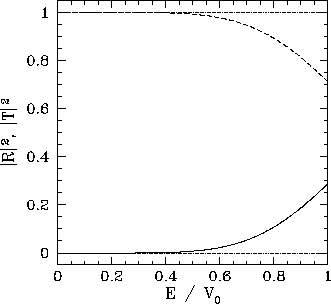
The reflection and transmission probabilities obtained from Eqs. (327) and (328), respectively, are plotted in Figs. 10 and
11. It can be seen, from Fig. 10, that the classical
result, ![]() and
and ![]() , is obtained in the limit where the height of the barrier
is relatively small (i.e.,
, is obtained in the limit where the height of the barrier
is relatively small (i.e., ![]() ). However, when
). However, when ![]() is
of order
is
of order ![]() , there is a substantial probability that the incident particle
will be reflected by the barrier. According to classical physics, reflection is impossible when
, there is a substantial probability that the incident particle
will be reflected by the barrier. According to classical physics, reflection is impossible when ![]() .
.
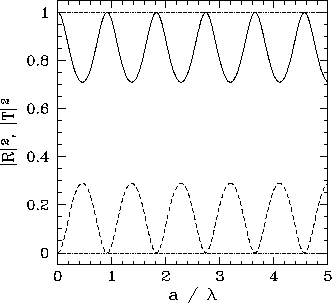
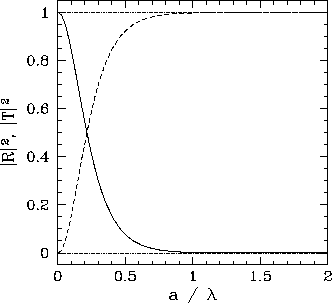
It can also be seen, from Fig. 11,
that at certain barrier widths the probability of reflection goes to zero. It turns out that this is true irrespective of the energy of the incident particle.
It is evident, from Eq. (327), that these special barrier widths
correspond to
| (329) |
Let us, now, consider the case ![]() . In this case, the general
solution to Eq. (320) inside the barrier takes the
form
. In this case, the general
solution to Eq. (320) inside the barrier takes the
form
| (330) |
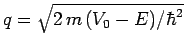 .
Continuity of
.
Continuity of | (331) | |||
| (332) |
| (333) | |||
| (334) |
It is again instructive to compare the quantum mechanical probabilities
of reflection and transmission--(335) and (336), respectively--with those derived from classical physics. Now, according
to classical physics, if a particle of energy ![]() is incident on
a potential barrier of height
is incident on
a potential barrier of height ![]() then the particle is reflected.
In other words, the classical probability of reflection is
unity, and the classical probability of transmission is zero.
then the particle is reflected.
In other words, the classical probability of reflection is
unity, and the classical probability of transmission is zero.
 |
 |
The reflection and transmission probabilities obtained from Eqs. (335) and (336), respectively, are plotted in Figs. 12 and
13. It can be seen, from Fig. 12, that the classical
result, ![]() and
and ![]() , is obtained for relatively
thin barriers (i.e.,
, is obtained for relatively
thin barriers (i.e., ![]() ) in the limit where the height of the barrier
is relatively large (i.e.,
) in the limit where the height of the barrier
is relatively large (i.e., ![]() ). However, when
). However, when ![]() is
of order
is
of order ![]() , there is a substantial probability that the incident particle
will be transmitted by the barrier. According to classical physics, transmission is impossible when
, there is a substantial probability that the incident particle
will be transmitted by the barrier. According to classical physics, transmission is impossible when ![]() .
.
It can also be seen, from
Fig. 13, that the transmission probability decays exponentially
as the width of the barrier increases. Nevertheless, even for very
wide barriers (i.e., ![]() ), there is a small but finite
probability that a particle incident on the barrier will be
transmitted. This phenomenon, which is inexplicable within
the context of classical physics, is called tunneling.
), there is a small but finite
probability that a particle incident on the barrier will be
transmitted. This phenomenon, which is inexplicable within
the context of classical physics, is called tunneling.